Entegrasyon ve Toplama Arasındaki Fark: Entegrasyon ve Toplama Karşılaştırması

içeren Entegrasyona karşı toplam ve alt sınırları olan ayrı değerleri içerir. Toplama

Lise matematiğinin üstünde, entegrasyon ve toplam sıklıkla matematiksel işlemlerde bulunur. Görünüşte farklı araçlar olarak ve farklı durumlarda kullanılırlar, ancak çok yakın bir ilişki içindedirler.

Toplama hakkında daha fazlası

Toplama, bir dizi sayı ekleme işlemi ve işlem genellikle Yunan sermaye harfi simgesi Σ ile gösterilir. Toplamı kısaltmak için kullanılır ve dizinin toplamına / toplamına eşittir. Esasen sonsuz sekansların özetlendiği diziyi temsil etmek için sıklıkla kullanılırlar. Vektörlerin, matrislerin veya polinomların toplamını belirtmek için de kullanılabilirler.

Toplama genelde ortak bir terime sahip bir dizi gibi genel bir terimle temsil edilebilen bir dizi değer için yapılır. Toplamın başlangıç ​​noktası ve bitiş noktası sırasıyla toplamın alt sınırı ve üst sınırı olarak bilinir.

Örneğin a ₁ , ₂ , ₃ , ₄ , …, ve n , 1 _{+ a} 2 _{+ a} 3 _{… + a} n ^{olup kolayca temsil edilebilir toplam notasyonunu Σ} _n i = 1 _a i

olarak kullanarak; Ben toplamın endeksi deniyor.

_{Uygulamaya dayalı toplam için birçok varyasyon kullanılır. Bazı durumlarda üst sınır ve alt sınır, Σ} 1≤i≤100 _a i _{ve Σ} i∈ [999] gibi bir aralık veya aralık olarak verilebilir [1, 100] _a i _{. Veya P, tanımlanmış bir küme olduğu Σ} i∈P _a i

gibi bir dizi küme olarak verilebilir.

_{Bazı durumlarda iki veya daha fazla sigma işareti kullanılabilir, ancak bunlar aşağıdaki gibi genelleştirilebilir; Σ} j _Σ k _a jk _{= Σ} j, k _a jk

.

Ayrıca, toplam çok sayıda cebirsel kuralları izler. Gömülü işlem ek olduğundan, cebirin ortak kurallarının birçoğu toplamların kendisine ve toplamın tasvir ettiği tek tek terimler için uygulanabilir.

Entegrasyon hakkında daha fazlası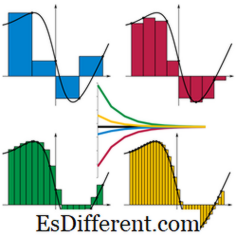

Entegrasyon, ters işlemin farklılaşması olarak tanımlanır. Fakat geometrik görünümünde, fonksiyon eğrisi ve eksen tarafından çevrelenen alan olarak da düşünülebilir. Bu nedenle, alanın hesaplanması diyagramda gösterildiği gibi kesin bir integralin değerini verir.

Resim Kaynağı: // tr. wikipedia. org / wiki / Dosya: Riemann_sum_convergence. png

Belirli integralin değeri aslında eğri ve eksen içindeki küçük şeritlerin toplamıdır.Her şerit alanı, dikkate alınan eksendeki noktadaki yükseklik × genişliktir. Genişlik, Δx değerini seçebildiğimiz bir değerdir. Ve yükseklik, yaklaşık olarak, düşünülen noktadaki fonksiyonun değeridir, örneğin f _(x i). Şemadan, şeritlerin küçük olması şeritlerin sınırlanan alanın içine sığması daha iyi, dolayısıyla değerin daha iyi bir şekilde yaklaştırılmasından daha iyi olduğu açıktır. Dolayısıyla, genel olarak, a ve b noktaları arasındaki (yani, [a, b] aralığında) belirli bir integral I (x xx (x 1 _n Δx, burada n şeritlerin sayısıdır (n = (ba) / Δx).Bu toplam alan toplamı, toplama notasyonu kullanılarak I ≅ Σ < Δx daha küçük olduğu zaman yakınlaştırma daha iyi olduğu için, Δx → 0 olduğunda (i _{Bu nedenle,} i f (x ^{= i} _{) Δx.} Yukarıdaki konseptten bir genelleme olarak, Δx'i, i tarafından endekslenen dikkate alınan aralığı temel alarak seçebiliriz (pozisyonun alanına göre alanın genişliğini seçerek) i = lim _{Δx → 0} Σ i <= 1 f _(x i ^{) Δx i} ₌ a ∫ _b f

(x) dx

Bu, Reimann İntegrali olarak bilinir. [a, b] aralığında f _{(x) işlevi. Bu durumda a ve b, integralin üst sınırı ve alt sınırı olarak bilinir. Reimann integrali tüm bütünleştirme yöntemlerinin temel bir şeklidir.} Özet olarak, entegrasyon dikdörtgenin genişliği sonsuz küçük olduğunda alanın toplamıdır. ^{Entegrasyon ve Toplama arasındaki fark nedir?} _{• Toplama, bir dizi sayı ekler. Genellikle toplam, dizideki terimler bir desene sahip olduğunda ve genel bir terim kullanılarak ifade edilebildiğinde, bu formda Σ} n i = 1 _a i _{şeklinde verilir.} • Entegrasyon temel olarak fonksiyon eğrisi, eksen ve üst ve alt limitlerle sınırlandırılan alandır. Bu alan, sınırlı alana dahil edilen çok daha küçük alanların toplamı olarak verilebilir. _{• Toplama, üst değer ve alt sınır değerleri ile ayrık değerleri içerir; oysa entegrasyon sürekli değerleri içerir.} • Entegrasyon, özel bir toplama biçimi olarak yorumlanabilir. ^{• Sayısal hesaplama yöntemlerinde, entegrasyon her zaman bir toplam olarak gerçekleştirilir.}