Güç Serileri ve Taylor Serileri Arasındaki Fark
'a kadar olan bir fonksiyondur. Güç Serileri vs Taylor Serisi
Matematiğin gerçek bir dizisi, reel sayıların sıralı bir listesidir. Resmen, doğal sayı kümesinden gerçek sayı kümesine kadar bir işlevdir. a n , bir dizinin inci terimiyse, sırayı a 1 , a 2 , …, a n, …. Örneğin, 1, ½, ⅓, …, 1 / n … dizisini göz önünde bulundurun …. {1 / n} olarak gösterilebilir.
Dizileri kullanarak bir dizi tanımlamak mümkündür. Bir dizi, bir dizinin koşullarının toplamıdır. Bu nedenle, her bir sekans için, bir ilişkili sekans vardır ve bunun tersi de geçerlidir. Eğer {a n> göz önüne alınmış dizilimse, o sıra tarafından oluşturulan diziler şu şekilde temsil edilebilir:
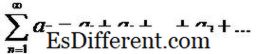
Böylece, yukarıdaki örnekte, ilişkili seriler 1+ 1 / 2 + 1 / 3 + … + 1 / n + ….
Adlardan da anlaşılacağı üzere, güç serisi özel bir dizi seridir ve Sayısal Analiz ve ilgili matematiksel modellemede yaygın olarak kullanılır. Taylor serisi, iyi bilinen fonksiyonları temsil etmenin alternatif ve kolay uygulanabilir bir yolunu sağlayan özel bir güç serisidir.
Power serisi nedir?
Bir güç serisi,
-- c
'da ortalanmış bir aralık için yakınsak (muhtemelen) olan - 1 ->. a n katsayıları gerçek veya kompleks sayılar olabilir ve x'den bağımsızdır; ben. e. kukla değişkeni. Örneğin her
n, ve c = 0 için a n = 1 ayarlayarak, güç serisi 1 + x + x 2 + … + x n + … elde edilir. X ∈ (-1, 1) olduğunda bu güç serisinin 1 / (1-x) 'e yakınsak olduğunu gözlemlemek kolaydır.
x = c olduğunda güç serileri yakınsar. Gç serilerinin yakınsadığı x diğer değerleri daima c merkezli açık aralık şeklinde olacaktır.,, her x için xc | ≤ R olan 0≤ R ≤ ∞ değeri olacaktır >, güç serileri yakınsaktır ve her x | xc |> R için güç serileri farklıdır. Bu değer R, güç serisinin yakınsama yarıçapı olarak adlandırılır (R gerçek değer veya pozitif sonsuzluğu alabilir). 3'ten büyük -> Güç serileri, aşağıdaki kuralları kullanarak eklenebilir, çıkarılabilir, çarpılır ve bölünebilir. İki güç serisini düşünün:.
Sonra,

gibi terimler eklenir veya birlikte çıkarılır. Ayrıca, iki kuvvet serisini,
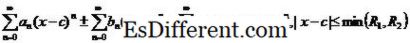
Taylor serisi, bir aralıkta sonsuz diferensiyellenebilen f

(
x) bir işlev için tanımlanır. f (x), c merkezli bir aralıkta tayin edilebileceğini varsayıyoruz. Sonra Tarafından verilen güç dizisi! - 3 ->, f
(
x) işlevinin Taylor serisi genişlemesi olarak adlandırılır. C. ((999) (c ) x c ). Sayısal Analizde, sonsuz genişlemedeki sonlu sayıda terim, serinin orijinal işleve yakınsadığı noktalardaki değerlerin hesaplanmasında kullanılır. Her x ∈ (a, b) aralığında (a, b) aralıkta bir f
(x) fonksiyonunun analitik olduğu söylenir), f (x) Taylor serisi f (x) işlevine yakınsar. Örneğin, Taylor genişlemesinin 1 + x + x 2 + … + x n + … yakınsaması nedeniyle, 1 / (1-x) (-1, 1) e x 'un Taylor serisi e x e yakınsaklığına göre, o aralıktaki işleve ve e x her gerçek sayı için x. Power serisi ile Taylor serisi arasındaki fark nedir? 1. Taylor serisi, yalnızca açık aralıklarla sonsuz diferensiyellenebilir fonksiyonlar için tanımlanmış özel bir güç serisidir. 2. Taylor serisi
özel formunu alırken, bir güç serisi
Serisinin herhangi bir serisi olabilir. --2 ->



