Centroid Circccenter Incenter ve Orthocenter Arasındaki Fark | Centroid vs Circumcenter vs Incenter vs Ortossent
Circumcenter, Incenter, Orthocenter vs Centroid
Circumcenter: circumcenter üçgen 'daki üç dikey bisectors'ın kesişim noktasıdır. Circumcenter circumcircle 'un merkezi olup, üçgen üç köşesinden geçen bir daire.

Sünnetci çizmek için üçgenin kenarlarına dikey ikigenler oluşturun. Kesişme noktası, sünnetçiyi verir. Püskürtmeyi ve cetvelin düz kenarını kullanarak bir bisector oluşturulabilir. Pusulayı, çizgi parçasının uzunluğunun yarısından daha fazla bir yarıçapa ayarlayın. Ardından, bir ucunu yayın merkezi olacak şekilde parçanın iki yanında iki tane kemer yapın. İşlemi, parçanın diğer ucuyla tekrarlayın. Dört tane yay, segmentin iki tarafında da iki kesişme noktası oluşturur. Cetvel yardımı ile bu iki noktayı birleştiren bir çizgi çizin ve bu, kesitin dikey çiftektörünü verecektir.

Çevrelere yaratmak için, merkezci olarak daireyi çizin ve daire başı ile vertex arasındaki uzunluğu dairesel yarıçapı olarak çizin.
Incenter: Incenter, üç açı ikiyeri s 'un kesişme noktasıdır. Incenter üçgenin üç yanını kesen çevreye dairenin ortasındadır.
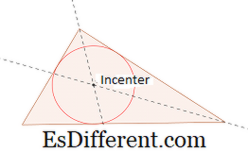
Üçgenin eğimini çizmek için üçgeninin her iki iç açırayektörünü oluşturun. İki açılı bisectors'ın kesişme noktası incenter verir. Açı açıortayını çizmek için, her bir kol üzerinde aynı yarıçapa sahip iki adet yay oluşturun. Bu, açının kollarında iki nokta (her bir kolda bir tane) sağlar. Ardından, kollardaki her bir noktayı merkezler olarak alarak iki tane daha kemer çizin. Bu iki yayın kesişimi tarafından oluşturulan nokta üçüncü bir noktayı verir. Açının ve üçüncü noktanın tepe noktasını birleştiren bir çizgi, açıyla açıortayı verir.
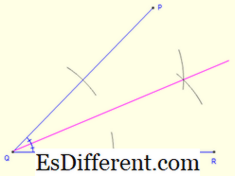
İncircle 'ı oluşturmak için, incenter'ten geçen herhangi bir kenara dik bir çizgi segmenti oluşturun. Dikey tabanı ile eğimlendiricinin yarıçapı arasındaki uzunluğu alarak komple bir daire çizin.
Orthocenter: Orthocenter, üçgenin üç yüksekliğinin (yüksekliklerin) kesişim noktasıdır.

Ortocenter oluşturmak için üçgen bir rakımını çizin. Karşıt köşeden geçen bir kenara dik olan bir çizgi parçasına bir yükseklik denir.Bir noktadan geçen dikey bir çizgi çizmek için, önce noktayı merkez olarak çizgide iki yay oluşturun. Ardından, kesişim noktalarının her biri merkez olarak olacak şekilde iki tane daha oluştur. İlk noktayı birleştiren ve son olarak oluşturulan bir noktayı birleştiren bir çizgi parçasını çizin ve çizgiyi çizgi parçasına dik olacak ve ilk noktadan geçeceksiniz. İki yüksekliğin kesişim noktası ortocenter verir.
Centroid: Centroid, bir üçgeninin üç medyanının kesişim noktasıdır. Centroid, her medyanı 1: 2 oranına böler ve üniform, üçgen bir tabakanın kütle merkezi bu noktada bulunur.

Yüzeyi belirlemek için, üçgenin herhangi iki orta değerini oluşturun. Medyan oluşturmak için, bir tarafın orta noktasını işaretleyin. Daha sonra orta noktayı ve üçgenin karşıt köşesini birleştiren bir çizgi segmenti oluşturun. Medyanların kesişim noktası üçgenin simgesini verir.
Circumcenter, Incenter, Orthocenter ve Centroid arasındaki farklar nelerdir?
• Dairesel merkez üçgenin dikey bisectors'ı kullanılarak oluşturulmuştur.
• Üç boyutlu açıların ikiye bölgeleri kullanılarak sintanlar oluşturulur.
• Ortagonel, üçgenin yüksekliklerini (rakımları) kullanarak yaratılmıştır.
• Centroid üçgenin medyan değerlerini kullanarak yaratılır.
• Hem sörünç hem de eğlendirici belirli geometrik özelliklere sahip çevreleri ilişkilendirir.
• üçgeninin geometrik merkezidir ve düzgün üçgen tabaka kütlesinin merkezidir.
• Eşit olmayan bir üçgen için, sünnet yeri, ortocenter ve merkez çizgi düz bir çizgide bulunur ve çizgi Euler çizgisi olarak bilinir.




