Paralelkengraf ile Dörtgen arasındaki fark: Paralelkenar Çizgiye Göre Dörtlü

Paralelkenar vs Dörtlügen < Dörtgenler ve paralelkenarolar Öklid Geometrisinde bulunan poligonlardır. Paralelkenar dörtlü bir özel durumdur. Dörtgenler düzlemsel (2D) veya 3 Boyutlu olabilirken paralelkenarolar daima düzlemsel olabilir.

Dörtlü

Dörtlü, dört kenarlı bir çokgentir. Dört tane köşe bulunur ve iç açıların toplamı 3600'dür (2π rad). Dörtgenler kendinden kesişen ve basit dörtgen kategorilere ayrılır. Kendi kesişen dörtgenler iki veya daha fazla kenarı birbirine geçer ve daha küçük geometrik şekiller (üçgen gibi üçgenler oluşur).

Basit dörtlü kenarlar da konveks ve konkav dörtlügenlere ayrılmıştır. İçbükey dörtgenler, şekil içinde refleks açılar oluşturan bitişik yanlara sahiptir. İçinde refleks açısı olmayan basit quadrilateraller dışbükey dörtgenlerdir. Dışbükey dörtgenler herzaman tezeli olabilir.

Dörtlüklerin geometrilerinin başlangıç ​​seviyelerindeki önemli bir kısmı dışbükey dörtgenler ile ilgilidir. Bazı dörtgenler ilkokul çağlarından beri çok tanıdık gelir. Aşağıda, farklı konveks dörtgenler gösteren bir diyagram bulunmaktadır.

Parallelogram

Paralelkenar dört taraflı geometrik şekil olarak, zıt yanları birbirine paralel olarak tanımlanabilir. Daha doğrusu, iki paralel kenar çiftiyle dörtlü bir bölgedir. Bu paralel doğa, paralelogramlara birçok geometrik karakteristik verir.

Aşağıdaki dört geometrik karakteristiklerin bulunması durumunda, dörtgen bir paralelkenar.

• İki çift karşı taraf uzunluğu eşittir. (AB = DC, AD = BC)

• İki çift karşıt açı boyutu eşittir. ()

• Bitişik açıların tamamlayıcı olması

• Birbirine karşıt olan bir çift yan uzunluk eşit ve paraleldir. (AB = DC & AB‖DC)

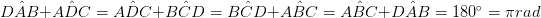
• Çaprazlıklar birbirlerini ikiye bölür (AO = OC, BO = OD)

• Her bir diyagonal, dörtlüü iki uyumlu üçgene böler. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Ayrıca, kenarların karelerinin toplamı diyagonallerin karelerinin toplamına eşittir. Bu, bazen

paralelogram yasası olarak anılır ve fizikte ve mühendislikte yaygın uygulamalar içerir. 2 2 ^{= AC} 2 ^{+ BD} 2 ⁺ 2 ⁾ Yukarıdaki özelliklerin her biri özellik olarak kullanılabilir, bir kere dört kenarlığın bir paralelkenogram olduğu tespit edilir. ^{Parlaklık görüntüsünün alanı, bir tarafın uzunluğu ve karşı tarafın yüksekliği çarpımı ile hesaplanabilir. Bu nedenle, paralelkenogramın alanı} olarak verilebilir. Parlaklık alanı alanı = taban × yükseklik = ^AB ×

h

Paralelkenogramın alanı, tek paralelkenarogramın şekline bağlı değildir. Sadece taban uzunluğuna ve dikey yüksekliğe bağlıdır.

Bir paralelkenarın kenarları iki vektörle temsil edilebiliyorsa, alan, iki bitişik vektörün vektör ürününün büyüklüğü (çarpım çarpımı) ile elde edilebilir. Yan AB ve AD sırasıyla vektörler () ve () ile temsil edilirse, paralelkenogramın alanı

ile verilir; burada α, ve arasındaki açıdır >.

Aşağıda, paralelkenogramın bazı gelişmiş özellikleri verilmiştir;

• Bir paralelkenogram alanı, köşegenlerinden herhangi birinin oluşturduğu bir üçgen alanının iki katıdır.

• Paralelkenogramın alanı, orta noktadan geçen herhangi bir çizgi ile yarısına bölünür.

• Herhangi bir dejenere olmayan afin dönüşümü, başka bir paralelkenaraya paralel •

• Bir paralelkenar, 2

dereceli dönme simetriye sahiptir. • Paralelkenarşanın iç noktalarından yanlara olan mesafelerin toplamı bağımsızdır noktanın konumu

Parallelogram ve Quadrilateral arasındaki fark nedir?

• Quadrilateraller, dört kenarlı poligonlardır (bazen tetragon olarak adlandırılır), paralelkenar dörtlü bir özel tiptir.

• Quadrilateraller, kenarlarını farklı düzlemlerde (3d uzayda) alabilir; bu arada, paralelkenarogramın tüm kenarları aynı düzlemde (düzlemsel / 2 boyutlu) bulunur.

• Dörtlü kenarlı iç açılar 3600'e kadar toplamayı sağlayacak herhangi bir değeri (refleks açılar dahil) alabilir. Paralellikler maksimum açı şekli olarak sadece ufak açılara sahip olabilir.

• Kare kenarın dört yüzü farklı uzunluklarda olabilirken, paralelkenarogramın karşı tarafları daima birbirine paralel ve uzunluğuna eşittir.

• Herhangi bir diyagonal, paralelkenizi iki uyumlu üçgen içine bölünürken, genel bir dörtlü kenarlı köşegen tarafından oluşturulan üçgenler mutlaka uyumludur.