Türev ve Diferansiyel Arasındaki Fark

Türev ve Diferansiyel

kullanılır. Diferansiyel denklemde, bir fonksiyonun türevi ve diferansiyelleri birbirine yakındır ancak çok farklı anlamlara sahiptirler ve türevlenebilir işlevlerle ilgili iki önemli matematiksel nesneyi temsil etmek için kullanılır.

Türev nedir?

Bir fonksiyonun türetilmesi, fonksiyonun değerinin girişi değiştikçe değişme oranını ölçer. Çok değişkenli fonksiyonlarda, fonksiyon değerindeki değişiklik, bağımsız değişkenlerin değerlerinin değişim yönüne bağlıdır. Bu nedenle, bu gibi durumlarda, belirli bir yön seçilir ve fonksiyon, o belirli yönde farklılaştırılır. Bu türe directional türev denir. Kısmi türevler yön türevlerinin özel bir türüdür.

Vektör değerli bir fonksiyonun türevlendirmesi f sonlu olarak nerede olursa olsun sınır

olarak tanımlanabilir. Daha önce de belirtildiği gibi, bize u vektörü yönünde f işlevinin artış oranını verir. Tek değerli bir fonksiyon söz konusu olduğunda, türevin bilinen tanımına,

Örneğin,

her yerde türevlenebilir ve türevi

sınırına eşittir, bu

e eşittir.

gibi fonksiyonların türevleri her yerde mevcuttur. Bunlar sırasıyla

işlevlerine eşittir.

Bu ilk türev olarak bilinir. Genellikle f işlevinin ilk türevi f ⁽¹⁾ ile gösterilir. Şimdi bu gösterimi kullanarak, yüksek mertebeden türevleri tanımlamak mümkündür.

f ⁽ n ⁿ türevlerini her 999 ile ifade eden ikinci dereceden yönsel türevidir) n,

, n ^inci türevini tanımlar.

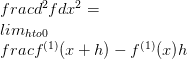
Diferansiyel nedir?

Bir fonksiyonun diferansiyel, bağımsız değişken veya değişkenlerin değişimine göre fonksiyondaki değişikliği temsil eder. Normal gösterimde, x tek bir değişkenin f belirli bir fonksiyonu için, 1 df derecesinin toplam diferansiyel değeri tarafından verilen olur. Bu,

x daki (yani d x) sonsuz küçük bir değişim için, f (1) ⁽ x) d x daki değişiklik f. Sınırları kullanmak, bir tanımı şu şekilde sona erdirebilir.

x rasgele bir noktada x daki değişiklik ve x işlevinde karşılık gelen değişiklik olduğu varsayıldığında, f. Δ f = f (1) ( ^x ) Δ x + ε, olduğu gösterilebilir; burada ε hata. Şimdi Δ x → 0 Δ f ^{/ Δ} x _{= f} (1) sınırı Δ x 0 ^ε / Δ x (daha önce belirtilen türev tanımı kullanılarak)> (x > = 0.Bu nedenle Δ ^{x →} 0 _{ε = 0 olduğu sonucuna varmak mümkündür. Şimdi, Δ} x → 0 Δ f d f ve Δ x → 0 Δ x d x olarak diferansiyel tanımı titizlikle elde edilir. Örneğin, işlevinin diferansiyel değeri 'dır. İki veya daha fazla değişken fonksiyonlarında bir fonksiyonun toplam diferansiyeli, bağımsız değişkenlerin her birinin yönündeki diferansiyellerin toplamı olarak tanımlanır. Matematiksel olarak olarak belirtilebilir.

Türev ve diferansiyel arasındaki fark nedir?

• Türev bir fonksiyonun bir değişim oranını ifade eder; diferansiyel ise, bağımsız değişken değişmeye maruz kaldığında, fonksiyonun gerçek değişimine atıfta bulunur.

• Türev

ile verilir, ancak diferansiyel

ile verilir.

Önerilen Karayipler ve Bahamalar Arasında farkı Kariyer ve İş Arasındaki Fark Caribou ve Reindeer arasındaki fark