Belirli ve Belirsiz İntegral Arasındaki Fark
olarak bilinir. Matematik, matematiğin önemli bir koludur ve diferansiyasyon, hesaplamada kritik bir rol oynamaktadır. Türevin ters işlemi bütünleme olarak bilinir ve ters, integral olarak bilinir veya basitçe ifade edilirse, türevin tersi bir integral verir. Ürettikleri sonuçlara dayanarak integraller iki sınıfa ayrılırlar., kesin ve belirsiz integraller.
Kesin İntegral
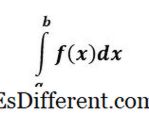
f (x) 'un kesin integrali bir NUMARA ve f (x) eğrisinin altındaki alanı temsil eder. x = a, x = b için.
Kesirli integralin, integraller üzerinde üst ve alt limitleri vardır ve kesin olarak adlandırılır çünkü problemin sonunda, bir sayımız vardır - kesin bir cevaptır.
Belirsiz İntegral

f (x) 'in belirsiz integrali bir FONKSİYON ve "Farklılaştırıldığında hangi fonksiyon f (x) ' ı verir? "
Belirsiz integral ile burada integralin üst ve alt sınırları yoktur ve elde edeceğimiz şey yine de x olan bir cevaptır ve aynı zamanda sabit (genellikle C ile gösterilir).
Belirsiz integral genellikle diferansiyel denklemin genel bir özümünü verir.
Belirsiz integral, genel bir entegrasyon biçiminden daha fazla ve dikkate alınan fonksiyonun anti-türevi olarak yorumlanabilir.
Fonksiyonun farklılaştırılmasının F başka bir fonksiyona f yol açtığını ve f'nin integralinin integrali verdiğini varsayalım. Sembolik olarak, hem
F
hem de
ƒ
F
İntegraller ve entegrasyon süreci, diferansiyel denklemlerin özümünde kalibredir. Bununla birlikte, farklılaşmanın basamaklarının aksine, entegrasyon adımları her zaman açık ve standart bir yordamı takip etmez. Bazen çözümün temel işlev açısından açıkça ifade edilemediğini görüyoruz. Bu durumda, analitik çözüm çoğunlukla belirsiz integral formunda verilir.
Calculus'un Temel Teoremi
Kesin ve belirsiz integral, Calculus'un Temel Teoremi ile bağlantılıdır:
Belirli integralin hesaplanması için, belirsiz integralin 'unu bulun > (anti-türev olarak da bilinir) ve x = a ve x = b bitiş noktalarında değerlendirilir. Belirli ve belirsiz integraller arasındaki fark, aynı işleve ait integralleri değerlendikten sonra açıkça görülecektir. Aşağıdaki integrali göz önünde bulundurun:
OK. İkisini de yapalım ve farkı görelim.
Entegrasyon için, dizine bir tane eklemeliyiz ki bu bize şu ifadeye yöneliyor:

Bu noktada
C
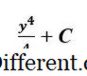
sadece bir sabittir. C kesin değerini belirlemek için sorunda ek bilgi gerekmektedir. Aynı integrali kesin formunda değerlendirelim i. e., üst ve alt sınırlar dahil edilmiştir. Grafik olarak konuşurken, y = 2

ve y = 3 arasındaki f (x) = y 3 eğrisinin altındaki alanı hesaplıyoruz >. Bu değerlendirmedeki ilk adım belirsiz integral değerlendirmesiyle aynıdır. Tek fark şu ki bu sefer C sabitini eklemiyoruz.
Bu durumda ifade şu şekilde görünür: Bu dönüş yol açar: Esasında, ifadede 3 ve ardından 2'yi ikame ettik ve aralarındaki farkı elde ettik.
Bu sabit

C

kullanımının aksine kesin değerdir.
Sabit faktörü (belirsiz integral ile ilgili olarak) biraz daha ayrıntılı olarak keşfedelim. y
3
diferansiyeli 3y 2 ise, o zaman ∫ 3y 2
dy = y 3 Ancak 3y 2 , bazıları y 3 -5 , > y 3 +7 , vb. Bu, işlem sırasında sabitin hesaba katılmadığı için tersinin benzersiz olmadığı anlamına gelir. Yani genel olarak, 3y 2 , 3 + C arasındaki farktır ve burada C sabittir. Bu arada, C, 'entegrasyon sabiti' olarak bilinir. Bunu şöyle yazacağız: ∫ 3y 2
. dx = y
3 + C Tablolar araması veya Risch entegrasyonu gibi belirsiz bir integral için entegrasyon teknikleri, entegrasyon işlemi sırasında yeni süreksizliklere neden olabilir. Bu yeni süreksizlikler, anti-türevler karmaşık logaritmalara ihtiyaç duyabileceği için ortaya çıkmaktadır. Kompleks logaritma, argüman negatif gerçek ekseni geçtiğinde sıçrama süreksizliğine sahiptir ve entegrasyon algoritmaları bazen bu atlamaların iptal edildiği bir gösterimi bulamazlar.


